FHQ Treap 详解

发表于 阅读次数：

1）FHQ-Treap 基本功能理论与实现

不同于经典的基于左旋、右旋的 Treap(Splay)，FHQ-Treap 是基于分裂与合并的的一种 Treap。虽然两者操作方式完全不同，但产生的结果是一样的。而且，FHQ-Treap 具有好写（打板子超快）、好理解（左旋右旋我到现在还没搞明白）以及可持久化、区间翻转、移动等等诸多优点。

（%%% FHQ 大佬）

接下来会详细介绍 FHQ-Treap。

1.1）FHQ-Treap 模型

首先，它是一个 Treap；其次，它是一个基于分裂+合并的 Treap。

比如，可以通过创建一个只有根节点的 Treap，然后再和原来的 Treap 合并，这就是插入节点。

再比如，可以通过分裂开 Treap，把某个节点分离开，合并其他的节点，这就是删除节点。

……如此好用、好理解的 FHQ-Treap 如何实现呢？

Treap 是什么？

了解 Treap，我么要先了解 BST：二叉搜索树。

BST 中，任意一个结点的左子树（假设它有）上所有点的值都比该点小，而右子树上所有点的值都该点大。由此可以得出，其中序遍历与所有结点上的值从小到大进行排序后的结果相同。该数据结构期望单次操作（插入/查询）的复杂度为 $\mathcal{O}(\log n)$，但是最坏情况下可以被卡到 $\mathcal{O}(n)$。

对此，我们可以使用随机化的思想，给每一个点附上一个随机的权值（或称优先级），通过维护优先级的方法来调整 BST 的形态，Treap 就是这一类数据结构。

众所周知，Treap 要维护的无非两点：

  1. 键值（key），满足：左儿子键值 $\leq$ 该节点键值 $\leq$ 右儿子键值

  2. 优先级（pri），满足：左儿子优先级或右儿子的优先级 $\leq$ 该节点的优先级。

其中，键值一般是我们需要维护的值，而优先级一般是为了平衡 BST 的形态、提高 Treap 效率而采用的。

我们需要在分裂操作与合并操作中根据这两点对 Treap 进行维护（因为其他操作都建立在这两个操作上）。

我们可以定义一个结构体，记录 Treap 上每个点的信息。

1
2
3
4
5
6
struct Node {
    int lsn,rsn;
    int key,pri,siz;
};
int tSize=0,root=0;
Node treap[MS];

其中 tSize 是节点个数，root 是 Treap 的根。这里使用了数组的方式存储 Treap。

1.2）操作一：分裂（Split）

Split 需要考虑四个参数，分别是当前遍历到的节点、分裂的标准、传递回的两棵树的根。

一般，Split 都是讲某个 Treap 分裂成一个小于等于某值的 Treap，一个大于该值的 Treap。

1
void split(int u,int x,int &L,int &R);

其中很妙的一点，$L$ 与 $R$ 都传递了它的地址，即可通过该操作修改某个 Treap 的左子树、右子树信息或传递回分裂开的两个 Treap 的编号。这一点在后面的应用中十分重要。

那么如何分裂呢？

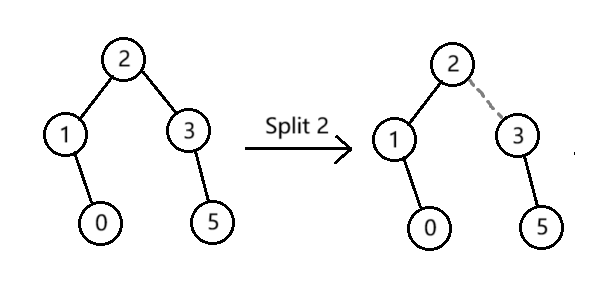
（这里分裂的操作并不用到优先级，节点上的值都是键值）

很明显的可以看出：

  • 当目前枚举到的 Treap 的根要小于等于分裂标准时，其左子树都必然小于等于分裂标准，只用考虑右子树；

  • 反之，当目前 Treap 的根要大于分裂标准是，其右子树必然都大于分裂标准，只用考虑左子树。

所以，代码就很明显了：

1
2
3
4
5
6
7
8
9
10
void split(int u,int x,int &L,int &R) {
    if(u==0) {
        L=R=0;
        return ;
    }
    if(treap[u].key<=x) L=u,split(treap[u].rsn,x,treap[u].rsn,R);
    else R=u,split(treap[u].lsn,x,L,treap[u].lsn);
    updateRoot(u);
    return ;
}

由于 Split 的时间复杂度就是树高，所以它的期望时间复杂度为 $\mathcal{O}(\log_2^n)$

1.3）操作二：合并（Merge）

划重点：Merge 的性质：Merge 要满足合并的两个 Treap （用根 L 与 R 表示），L 中的值都小于等于 R！

合并的时候，就要考虑优先值了。先比较两颗 Treap 的根节点的优先值大小。如果 L 大，把 R 合并到 L 的右子树上去；否则，把 L 合并到 R 的左子树上去（因为 L 中的值都小于 R）。最终，Merge 要返回合并后的根。

1
2
3
4
5
6
7
8
9
10
11
12
13
int merge(int L,int R) {
    if(L==0||R==0) return L+R;
    if(treap[L].pri>treap[R].pri) {
        treap[L].rsn=merge(treap[L].rsn,R);
        updateRoot(L);
        return L;
    }
    else {
        treap[R].lsn=merge(L,treap[R].lsn);
        updateRoot(R);
        return R;
    }
}

顺便说一下 updateRoot。用来更新某个节点为根的 Treap 的大小（求排名什么的要用到）。

1
2
3
4
void updateRoot(int u) {
    treap[u].siz=treap[treap[u].lsn].siz+treap[treap[u].rsn].siz+1;
    return ;
}

同上，期望时间复杂度 $\mathcal{O}(\log_2^n)$

$P.S.$ 到目前为止，FHQ-Treap 最难的部分都已经被你搞明白啦！剩下的都很简单的啦！

1.4）操作三：插入新节点

这很简单，首先创建一个只有一个节点的 Treap：

1
2
3
4
5
6
7
void makeNewNode(int x) {
    ++tSize;
    treap[tSize].siz=1;
    treap[tSize].lsn=treap[tSize].rsn=0;
    treap[tSize].key=x,treap[tSize].pri=rand();
    return ;
}

再把这个 Treap 合并到大 Treap 上：（注意 Merge 的性质，所以要先分裂）

1
2
3
4
5
6
7
int insert(int x) {
    int L,R;
    split(root,x,L,R);
    makeNewNode(x);
    root=merge(merge(L,tSize),R);
    return tSize;
}

1.5）删除某个节点

这里假设只删除一个与查询的值相通的节点。

先分裂出一颗全是要删除的值的 Treap，然后把这个 Treap 的左子树与右子树进行合并（把根丢掉），实现该操作。

1
2
3
4
5
6
7
8
int delNum(int x) {
    int L,M,R;
    split(root,x,L,R);
    split(L,x-1,L,M);
    M=merge(treap[M].lsn,treap[M].rsn);
    root=merge(merge(L,M),R);
    return root;
}

当然，如果你要一次性删除所有值为 $x$ 的节点，可以这么写：

1
2
3
4
5
6
7
int delNum(int x) {
    int L,M,R;
    split(root,x,L,R);
    split(L,x-1,L,M);
    root=merge(L,R);
    return root;
}

1.6）查询某个值的排名

不说了，把小于 $x$ 的分裂出来，它的大小加一。

1
2
3
4
5
6
7
int getRank(int x) {
    int L,R,res;
    split(root,x-1,L,R);
    res=treap[L].siz+1;
    root=merge(L,R);
    return res;
}

1.7）查询排名为 $k$ 的值

很好理解。

1
2
3
4
5
int kth(int u,int k) {
    if(k==treap[treap[u].lsn].siz+1) return u;
    if(k<=treap[treap[u].lsn].siz) return kth(treap[u].lsn,k);
    return kth(treap[u].rsn,k-treap[treap[u].lsn].siz-1);
}

1.8）查询 $x$ 的前驱与后继

见代码。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
// 前驱
int precursor(int x) {
    int L,R,res;
    split(root,x-1,L,R);
    res=treap[kth(L,treap[L].siz)].key;
    root=merge(L,R);
    return res;
}
// 后继
int successor(int x) {
    int L,R,res;
    split(root,x,L,R);
    res=treap[kth(R,1)].key;
    root=merge(L,R);
    return res;
}

1.9）End of this unit

以上就是所有 FHQ-Treap 的基本操作，接下来讲几个应用。

2）FHQ-Treap 的应用

2.1）洛谷 P3369

不说，套板子：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
#include <bits/stdc++.h>
using namespace std;

int n;
const int MS=100005;
struct Node {
    int lsn,rsn;
    int key,pri,siz;
};
int tSize=0,root=0;
Node treap[MS];
void makeNewNode(int x) {
    ++tSize;
    treap[tSize].siz=1;
    treap[tSize].lsn=treap[tSize].rsn=0;
    treap[tSize].key=x,treap[tSize].pri=rand();
    return ;
}
void updateRoot(int u) {
    treap[u].siz=treap[treap[u].lsn].siz+treap[treap[u].rsn].siz+1;
    return ;
}
void split(int u,int x,int &L,int &R) {
    if(u==0) {
        L=R=0;
        return ;
    }
    if(treap[u].key<=x) L=u,split(treap[u].rsn,x,treap[u].rsn,R);
    else R=u,split(treap[u].lsn,x,L,treap[u].lsn);
    updateRoot(u);
    return ;
}
int merge(int L,int R) {
    if(L==0||R==0) return L+R;
    if(treap[L].pri>treap[R].pri) {
        treap[L].rsn=merge(treap[L].rsn,R);
        updateRoot(L);
        return L;
    }
    else {
        treap[R].lsn=merge(L,treap[R].lsn);
        updateRoot(R);
        return R;
    }
}
int insert(int x) {
    int L,R;
    split(root,x,L,R);
    makeNewNode(x);
    root=merge(merge(L,tSize),R);
    return tSize;
}
int delNum(int x) {
    int L,M,R;
    split(root,x,L,R);
    split(L,x-1,L,M);
    M=merge(treap[M].lsn,treap[M].rsn);
    root=merge(merge(L,M),R);
    return root;
}
int getRank(int x) {
    int L,R,res;
    split(root,x-1,L,R);
    res=treap[L].siz+1;
    root=merge(L,R);
    return res;
}
int kth(int u,int k) {
    if(k==treap[treap[u].lsn].siz+1) return u;
    if(k<=treap[treap[u].lsn].siz) return kth(treap[u].lsn,k);
    return kth(treap[u].rsn,k-treap[treap[u].lsn].siz-1);
}
int precursor(int x) {
    int L,R,res;
    split(root,x-1,L,R);
    res=treap[kth(L,treap[L].siz)].key;
    root=merge(L,R);
    return res;
}
int successor(int x) {
    int L,R,res;
    split(root,x,L,R);
    res=treap[kth(R,1)].key;
    root=merge(L,R);
    return res;
}

int main() {
    scanf("%d",&n);
    while(n--) {
        int opt,x;
        scanf("%d%d",&opt,&x);
        if(opt==1) insert(x);
        if(opt==2) delNum(x);
        if(opt==3) printf("%d\n",getRank(x));
        if(opt==4) printf("%d\n",treap[kth(root,x)].key);
        if(opt==5) printf("%d\n",precursor(x));
        if(opt==6) printf("%d\n",successor(x));
    }
    return 0;
}

2.1）洛谷 P3391

翻转参考线段树的 lazy_tag。分裂的时候要稍微改一下，和查询排名一样。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
#include <bits/stdc++.h>
using namespace std;

int n,m;
const int MS=100005;
struct Node {
    int lsn,rsn;
    int key,pri,siz;
    int lazy;
};
int tSize=0,root=0;
Node treap[MS];
void makeNewNode(int x) {
    ++tSize;
    treap[tSize].siz=1;
    treap[tSize].lazy=treap[tSize].lsn=treap[tSize].rsn=0;
    treap[tSize].key=x,treap[tSize].pri=rand();
    return ;
}
void updateRoot(int u) {
    treap[u].siz=treap[treap[u].lsn].siz+treap[treap[u].rsn].siz+1;
    return ;
}
void pushDown(int u) {
    if(treap[u].lazy) {
        swap(treap[u].lsn,treap[u].rsn);
        treap[treap[u].lsn].lazy^=1;
        treap[treap[u].rsn].lazy^=1;
        treap[u].lazy=0;
    }
    return ;
}
void split(int u,int x,int &L,int &R) {
    if(u==0) {
        L=R=0;
        return ;
    }
    pushDown(u);
    if(treap[treap[u].lsn].siz+1<=x)
        L=u,split(treap[u].rsn,x-treap[treap[u].lsn].siz-1,treap[u].rsn,R);
    else R=u,split(treap[u].lsn,x,L,treap[u].lsn);
    updateRoot(u);
    return ;
}
int merge(int L,int R) {
    if(L==0||R==0) return L+R;
    if(treap[L].pri>treap[R].pri) {
        pushDown(L);
        treap[L].rsn=merge(treap[L].rsn,R);
        updateRoot(L);
        return L;
    }
    else {
        pushDown(R);
        treap[R].lsn=merge(L,treap[R].lsn);
        updateRoot(R);
        return R;
    }
}
void inorder(int u) {
    if(u==0) return ;
    pushDown(u);
    inorder(treap[u].lsn);
    printf("%d ",treap[u].key);
    inorder(treap[u].rsn);
    return ;
}

int main() {
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++) makeNewNode(i),root=merge(root,tSize);
    while(m--) {
        int l,r;
        scanf("%d%d",&l,&r);
        int L,R,mid;
        split(root,r,L,R);
        split(L,l-1,L,mid);
        treap[mid].lazy^=1;
        root=merge(merge(L,mid),R);
    }
    inorder(root);
    return 0;
}

END

还有几个应用没更新……我懒狗，等以后吧